NEP Lighting Engine Part 1: Shaders and materials
This is the second installment in a four-part series on the lighting engine in my upcoming indie game, Non-Essential Personnel. If you ended up here first, maybe try starting at the beginning instead.
Making flat things look not flat
The first trick for the lighting engine in a 2D game is to make sprites look like they have some depth and not look like characters out of Flatland. One way to do this is by using pixel shaders on the GPU. The basic idea here is to pretend that the sprite actually has some kind of 3D shape, do lighting calculations in 3D, and then project the results back down onto the 2D sprite. Anton Kudin (who's developing MegaSphere) has a great tutorial for how to do this in Unity. The lighting in MegaSphere just looks gorgeous, but I'm using a custom engine instead of Unity, so I have a bit more flexibility and I took a slightly different approach.
One way to pretend a completely flat sprite actually has a 3D shape uses a technique called bump mapping. In a nutshell, a bump map is a kind of texture for the sprite, but instead of encoding the color of each pixel, the bump map encodes a kind of pretend z-coordinate. If you write that z-coordinate to the red channel of the texture, it might look something like this:
The bump map for our hero
character for this blog post, Joe.Clearly I'm a programmer and not an artist. =P
It's actually a composite of many different bump maps since Joe's sprite is made of different parts. One of these days, I should normalize the intensities for Joe's bump maps. Maybe tomorrow...
If we were playing some kind of space-battle game with Cylons, Joe's bump map might actually be a passable sprite. That's the magic of bump maps. You get so much visual information about 3D shape from so little actual information in the texture.
If you want to make a bump map for your sprite, you can get arbitrarily fancy. Techniques that require building a high-poly 3D model and then projecting off the z-information are actually pretty common. I'm lazy though and took the very very low-tech route instead. I just painted the bump maps using brushes in GIMP. Getting the bump maps for fleshy bits to look round was hard at first, but you get better with practice. Dodge and Burn are your friends. =)
How to use z information in lighting
Once you have your bump map and sprite texture, the rest of the lighting magic happens in fragment shaders. There are tons and tons of different ways to combine texture colors with z-information and most of them fall into a fancy-sounding category called Bidirectional Reflectance Distribution Functions. That's just a very compact way of saying these models care about the direction light is travelling, the direction of the observer, and whatever properties the material has that affect light intensity.
One universally-used material property is the surface normal, or which way the surface of the sprite is "facing" at each pixel. This is the part of your sprite off which the light actually reflects. Different functions care about different material properties, but the traditional Blinn-Phong model is very simple and only uses the surface normal and material colors. Non-Essential Personnel actually uses a modified version of Blinn-Phong, but before I get to the modifications, I'll start with the basics first. We already get material colors from the sprite's texture, so we just have to convert the z-information from our bump map into surface normals the shader can use. Again, there are lots of different ways do to that, but I like simple, so I went with this one:
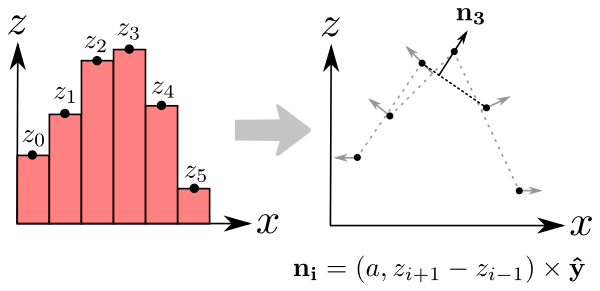Converting bump maps
to normal maps: The left side is the bump map. It just maps each pixel i to a height
zi. To make things simple, let's just pretend we have one-dimensional
sprites. The right side shows how to get the normals. To get the normal ni
for a pixel i, compute the slope from the heights of the neghboring pixels
zi+1 and zi-1. For the mathy readers, the equation shows how to do
that more precisely. y-hat is just notation for the unit y-axis. a is a meta parameter
that controls the "sensitivity" of your normals. A very small value (a=0.001)
makes the normals extremely sensitive to changes in height. i.e., small changes in the
bump map will make the sprite look like it has steep walls. A large value (a=1000) makes
the normals almost completely insensitive to height changes, meaning the sprite will
look pretty flat no matter what the bump map says. Remember, zi comes from a
texture, so the OpenGL driver will normalize it to the range [0,1]. This probably isn't
the most accurate way to compute normals, but it's really really cheap to compute in a
shader and the results look good enough for me.
It's worth mentioning here that many engines skip bump mapping entirely and just go straight to normal maps. Normal maps are just special textures that encode the surface normal directly instead of converting bump maps. The trouble is, they're much harder to create and require much more complicated tools than GIMP. For quick spriting, it's much easier to just paint a bump map and let the shader compute normals using a cheap heuristic.
But traditional Blinn-Phong lighting makes everything look like it's in space!
That's because traditional Blinn-Phong does a really poor job of modeling atmospheric scattering and reflections for backlighting. Most people work around this by using a constant "ambient" component, but I think that just looks awful too. There are always more complicated lighting models than Blinn-Phong (and better-looking ones too), but the good-looking ones generally have lots more parameters and are much more expensive to compute. Let's just tweak Blinn-Phong a bit and see if we can do better on the cheap.
The "diffuse" component of Blinn-Phong modulates light intensity by comparing the incoming light direction and the the surface normal using a very simple relationship:
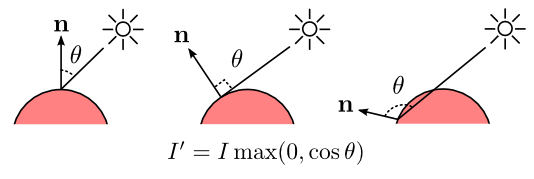Yeah, more
equations. I represents light intensity. Basically, the bigger the angle, the less light
gets through.
For extra fun, on the far right, theta is greater than 90 degrees and hence cos theta is less than zero. No light intensity survives in this case. It makes sense... I mean, light can't travel through a solid object, can it? Not unless you start getting really fancy, but let's keep things simple for now. We can get fancier later.
The trouble is, this lighting model makes the dark sides of objects look really dark. Like they were in space. That's great if you're making a space game, but the effect doesn't look right if you're making a game in a place that has an atmosphere. Turns out, lots of physical effects in terrestrial environments "spread out" the light and make shady spots quite a bit less dark. Light can bounce off of nearby surfaces and come back at the object from a different angle. If those reflective surfaces are actually atmospheric particles, the net effect is that light can "bend" around objects. It's actually compound scattering, but it's not horribly wrong to think of it as bending.
There are lots of complicated phenomena going on in atmospheres that a simple linear relationship with cos theta just doesn't capture. We could get super crazy and try to represent atmospheric properties in the shader, or go the global illumination route and let light bouce a few times before pretending it doesn't exist anymore. All of this stuff could get us really realistic lighting.
But I'm lazy. I like simple. Let's just start hacking the math until we find something that looks good.
The problem is the dark side of objects look too dark and that darkness looks too uniform. After all, we start ignoring any contribution from light after theta rises above 90 degrees.
Why not just stop ignoring the light after theta rises above 90 degrees?
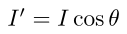Bam! Blinded with
math!
But we changed the range of diffuse contribution from [0,1] to [-1,1], so don't forget to renormalize:
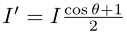Normalization is a
really useful life skill.
That one simple change makes a dramatic improvement in lighting:
The Goomba
looks a lot more scared now.
Easy enough, but what the heck does this have to do with modeling the atmosphere? What does that change mean in the physical world?
I said before that light can't travel through solid objects. However, this change means that we're saying light really can travel through solid objects in our virtual game world. Go back and stare at the far right of our light itensity figure above for a minute. We just stopped ignoring that case. Of course, in the real world, visible light can't travel through solid objects. At least, not far enough to notice with the naked eye.
Thankfully video games don't have to be perfectly realistic. We we get to cut corners.
The corner we just cut says that, yes we'll allow light to travel through solid objects and directly illuminate the "dark" side. So ... we just broke reality. But in exchange, we got dark side illumination without having to model complicated atmospheric effects. We just replaced that really complicated thing with a simple mathematical hack.
We approximated it!
If this were a science project, the next fun step would be to go measure lights in the real world and try to figure out how wrong our approximation is.
But this is a video game. Nobody cares. =P
Let's move on.
Materials encode all the physical properies of sprites we need for lighting
I spent quite a bit of space in this post talking about the diffuse lighting component of Blinn-Phong, and briefly mentioned the ambient component. Blinn-Phong also has a specular component that controls how shiny an object appears. Non-Essential Personnel uses that too, but I didn't mess around with it too much, so there's nothing exciting going on there.
I also added a material property which I'm calling "translucency" that tweaks the normalization of the diffuse component. There's nothing too exciting here either, so I won't explain it in the excruciating detail I did for other stuff. The main idea here is that fleshy bits should look a bit brighter than solid bits and the shadows should look a bit softer due to subsurface scattering. Again, I'm not modeling a staggering amount of subsurface geometry here, it's just another glorious math hack.
If you encode all these properties into the material texture, it looks something like this:
The final material kinda look
like a rejected power
ranger.
Putting it all together
That big black box
contains the properties of the lights themselves, which I haven't talked about at all in
this post.
Now we know how to shade a sprite based on light direction and material properties, but that's only part of the picture. I haven't mentioned how the lights are positioned, and where light intensity comes from at all. If you're interested in that, head over to the next post in this series.
